ㅇ 완전탐색이란?
가능한 모든 경우의수를 다 체크해서 정답을 찾는 방법. 3자리수 자물쇠가 있다면 000부터 999까지 모든 경우의수를 다 따져보는것이다.
이렇게 되면 효율성은 떨어질 수 있으므로 문제에 대한 파악이 중요하다.
ㅇ 완전탐색의 방법
- Brute Force : 반복/조건문을 활용해 모두 테스트하는 방법
- 순열 : n개의 원소중 r개의 원소를 중복허용없이 나열하는 방법
- 재귀 호출
- 비트 마스크 : 2진수 표현기법을 활용하는 방법
- BFS, DFS를 활용하는 방법
ㅇ Brute Force 기법
public class BruteForceExample {
public static void main(String[] args) {
int[] numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
for (int number : numbers) {
if (number % 2 == 0) {
System.out.println("짝수: " + number);
}
}
}
}간단히 이런식이다. 모든 수를 다 대입해봐서 조건에 맞으면 출력하는식이다.
ㅇ 순열(Permutation)
public class PermutationsExample {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
generatePermutations(arr, 0);
}
public static void generatePermutations(int[] arr, int currentIndex) {
if (currentIndex == arr.length - 1) {
// 배열의 끝까지 도달한 경우 순열 출력
System.out.println(Arrays.toString(arr));
} else {
for (int i = currentIndex; i < arr.length; i++) {
// 현재 인덱스와 i 위치의 원소 교환
swap(arr, currentIndex, i);
// 재귀 호출로 다음 위치의 순열 생성
generatePermutations(arr, currentIndex + 1);
// 다시 교환하여 원래 상태로 복구
swap(arr, currentIndex, i);
}
}
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}generatePermutaions 는 주어진 1,2,3 요소에대한 모든 순열을 생성하는 메서드다. 재귀를 써서 다음 위치의 순열을 생성하고 순서를 바꿔주는 swap 메서드를 사용해서 다시 복구한다.
출력은 {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 2, 1}, {3, 1, 2} 이렇게 나오게 된다.
ㅇ 재귀호출
public class RecursiveSumExample {
public static void main(String[] args) {
int n = 5; // 합을 구할 자연수 범위 (1부터 n까지)
int sum = calculateSum(n);
System.out.println("1부터 " + n + "까지의 합: " + sum);
}
public static int calculateSum(int n) {
if (n == 1) {
return 1; // 기저 조건: 1의 합은 1
} else {
return n + calculateSum(n - 1); // n과 n-1까지의 합을 재귀 호출을 통해 구함
}
}
}
이런식으로 재귀호출이 되면서 밑에서부터 올라오면 1+2+3+4+5 를 구하는 로직이 된다.
위에서부터 보면 5 + calculateSum(4) 는 5 + 4 + calculateSum(3) ...... 이런식.
ㅇ 비트마스크
https://thcoding.tistory.com/129
타겟넘버
이것도 완전탐색으로 풀어야겠다는 감이왔다. 어제 풀었던걸 응용해봐야겠다 싶다가 -인경우도 생각해봐야해서 다르게 생각했다. 재귀로도 물론 풀수 있지만 비트마스킹을 사용해 풀수도있다.
thcoding.tistory.com
비트마스크를 이용해 푼 문제다.
간단한 예제로는
public class BitmaskExample {
public static void main(String[] args) {
int N = 10; // 1부터 N까지의 자연수 중에서 짝수를 찾을 것입니다.
int bitmask = 0; // 비트마스크 초기화
// 1부터 N까지 반복
for (int i = 1; i <= N; i++) {
if (i % 2 == 0) {
// i가 짝수인 경우 해당 비트를 1로 설정
bitmask |= (1 << i);
}
}
// 짝수 출력
System.out.print("1부터 " + N + "까지의 짝수: ");
for (int i = 1; i <= N; i++) {
if ((bitmask & (1 << i)) != 0) {
System.out.print(i + " ");
}
}
}
}여기서 쓰인 연산자를 보면 bitmask |= (1 << i); 는 bitmask = bitmask | (1 << i) 라는뜻인데, "|"는 비트단위의 OR 이고, 두 정수를 한비트씩 비교하면서 양쪽 비트중 하나라도 1이면 결과가 1이고 나머지는 0을 반환하는것이다.
그리고 1 << i 는 시프트 연산으로 정수 a를 왼쪽으로 b비트만큼 이동한다는 뜻이다. i가 짝수일때 니깐 예를 들어 i가 2면,
1은 0001이고 이걸 왼쪽으로 두칸씩옮기면 0100 이 되며 4가된다. 즉 짝수일때만 해당 비트를 1로 설정한다.

솔직히 설명이 부족하니 타겟넘버 포스팅을 보자.
ㅇ DFS, BFS
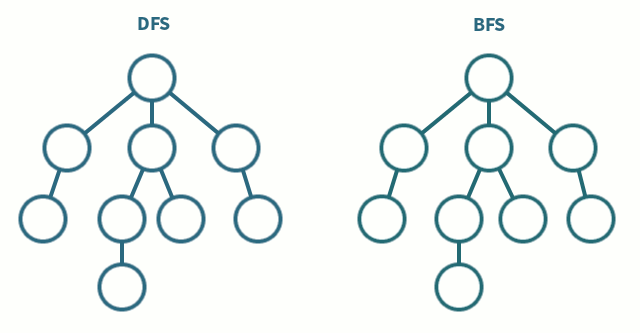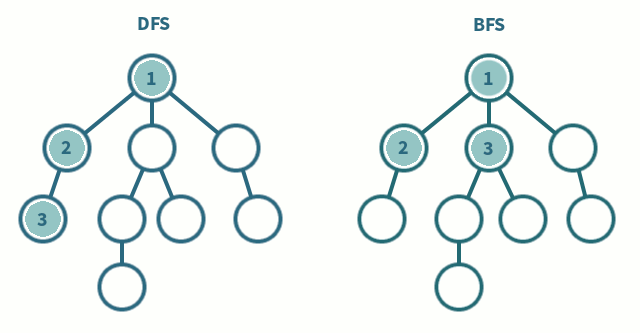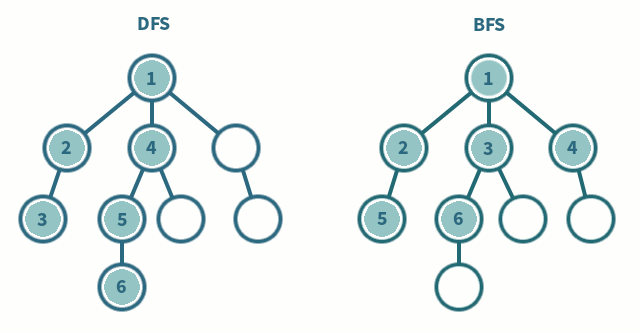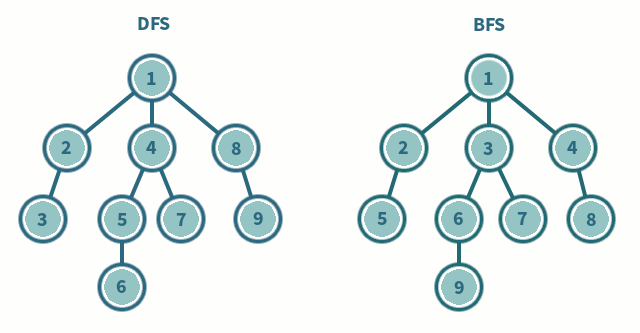
DFS는 말그대로 경로를 설정하고 한방향으로 쭉 들어갔다 나오고, BFS는 넓이를 기준으로 모든 경로를 탐색한다.
ㅇ BFS
BFS문제를 풀땐 거의 큐(Queue)를 사용한다.
위의 움짤을 보면 시작점을 큐에 삽입한다.
| 1 |
1을 제거하고 1과 간선이 연결된 2, 3, 4를 삽입
| 2 | 3 | 4 |
2를 제거하고 2와 간선이 연결된 5 삽입
| 3 | 4 | 5 |
3제거하고 3과 간선이 연결된 6, 7 삽입
| 4 | 5 | 6 | 7 |
4제거하고 4와 연결된 8삽입
| 5 | 6 | 7 | 8 |
5제거하고, 그다음 6제거하고 6과 연결된 9 삽입
| 7 | 8 | 9 |
그리고 7,8,9 순서대로 모두 제거된다.
bfs를 코드로 보자
/* 인접 리스트를 이용한 방향성 있는 그래프 클래스 */
class Graph {
private int V; // 노드의 개수
private LinkedList<Integer> adj[]; // 인접 리스트
/** 생성자 */
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i) // 인접 리스트 초기화
adj[i] = new LinkedList();
}
/** 노드를 연결 v->w */
void addEdge(int v, int w) { adj[v].add(w); }
/** s를 시작 노드으로 한 BFS로 탐색하면서 탐색한 노드들을 출력 */
void BFS(int s) {
// 노드의 방문 여부 판단 (초깃값: false)
boolean visited[] = new boolean[V];
// BFS 구현을 위한 큐(Queue) 생성
LinkedList<Integer> queue = new LinkedList<Integer>();
// 현재 노드를 방문한 것으로 표시하고 큐에 삽입(enqueue)
visited[s] = true;
queue.add(s);
// 큐(Queue)가 빌 때까지 반복
while (queue.size() != 0) {
// 방문한 노드를 큐에서 추출(dequeue)하고 값을 출력
s = queue.poll();
System.out.print(s + " ");
// 방문한 노드와 인접한 모든 노드를 가져온다.
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
// 방문하지 않은 노드면 방문한 것으로 표시하고 큐에 삽입(enqueue)
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
}
https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.htmlㅇ DFS
https://codingnojam.tistory.com/44
[Algorithm] DFS (Depth-first Search)를 Java로 구현해보자!
안녕하세요 Coding-Knowjam입니다. 오늘은 그래프와 트리를 탐색할 때 사용되는 DFS알고리즘에 대해서 알아보겠습니다. 1. DFS (Depth-first Search)란? DFS는 번역하면 깊이 우선 탐색이라고 합니다. 이름에
codingnojam.tistory.com
여기서 설명을 너무 잘해놓으셔서 이걸 보면 될것같다.
보통 DFS를 구현할땐, 스택이나, 재귀를 사용한다고 한다.
스택구현
public class DFSWithStack {
public void dfs(int[][] graph, int start) {
Stack<Integer> stack = new Stack<>();
boolean[] visited = new boolean[graph.length];
stack.push(start);
visited[start] = true;
while (!stack.isEmpty()) {
int node = stack.pop();
System.out.print(node + " ");
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
stack.push(neighbor);
visited[neighbor] = true;
}
}
}
}
}재귀구현
public class DFSWithRecursion {
public void dfs(int[][] graph, int node, boolean[] visited) {
visited[node] = true;
System.out.print(node + " ");
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
dfs(graph, neighbor, visited);
}
}
}
}



